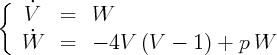
DU SYSTÈME DIFFÉRENTIEL
Le système différentiel :
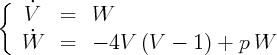
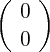 et
et 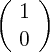 .
.
I- Étude du premier point fixe
La linéarisation au voisinage de l’origine donne la matrice 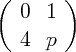 dont le
polynome caractéristique est :
dont le
polynome caractéristique est : 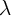 2 - p
2 - p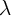 - 4 = 0 de discriminant positif, le produit des
racines étant négatif :
- 4 = 0 de discriminant positif, le produit des
racines étant négatif :
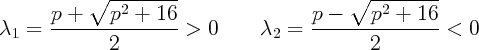

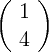 et
et 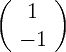 :
:
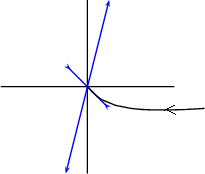
Le point fixe à l’origine est un point selle. Seule la solution Ce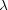 2u
2u 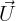 2 tend vers l’origine
quand u
2 tend vers l’origine
quand u  +
+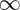 . Pour p = 3 la tangente à l’origine est alors la deuxième bissectrice.
. Pour p = 3 la tangente à l’origine est alors la deuxième bissectrice.
En remontant en sens inverse pour u, cette solution est la seule (p est quelconque et n'est pas forcément égal à 3) à donner un mascaret
avançant sans se déformer.
II- Étude du deuxième point fixe
V  1 V = 1 +
1 V = 1 + 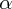
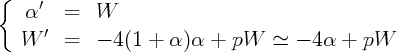
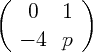 qui donne
qui donne 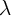 2 - p
2 - p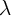 + 4 = 0.
+ 4 = 0.  = p2 - 16 .
p > 4. S > 0 P > 0
= p2 - 16 .
p > 4. S > 0 P > 0 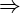
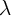 1 et
1 et 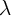 2 > 0 point fixe instable.
2 > 0 point fixe instable.
p < 4 S réelle positive, 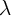 1 et
1 et 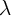 2 complexes conjuguées avec la même partie
réelle positive
2 complexes conjuguées avec la même partie
réelle positive 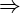 Spirale instable.
Spirale instable.
Notons que pour intégrer numériquement le système, il faut partir de l’origine, en
remontant vers les u décroissants, car on est alors sûr de converger rapidement vers le
mode stable (le seul à donner un mascaret) qui dans ce sens devient le seul mode
instable. La composante de la solution sur 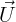 1 tend rapidement vers 0. On a donc pris
du négatif dans l’intégration numérique, et on part de l’origine suivant la deuxième
bissectrice.
1 tend rapidement vers 0. On a donc pris
du négatif dans l’intégration numérique, et on part de l’origine suivant la deuxième
bissectrice.
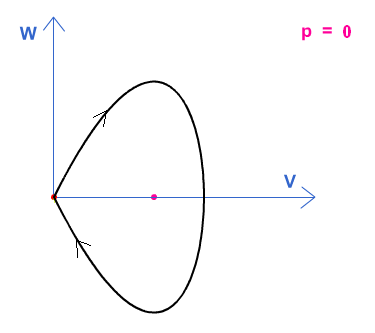
III- Étude du cas p = 0
Rappelons que dans l’équation différentielle, p > 0. Le système différentiel devient :
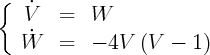
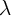 2 = -4,
2 = -4, 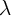 = ±2i pour le deuxième point fixe qui devient donc un
centre.
= ±2i pour le deuxième point fixe qui devient donc un
centre.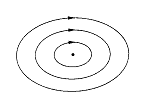
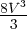 - W2 se conserve.
- W2 se conserve.
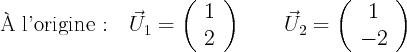
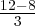 =
= 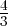 > 0. Le flot
tourne donc autour de ce point. Partons de O dans les sens des u croissants, par le
vecteur
> 0. Le flot
tourne donc autour de ce point. Partons de O dans les sens des u croissants, par le
vecteur 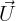 1 correspondant à la variété instable. W > 0, donc V augmente.
1 correspondant à la variété instable. W > 0, donc V augmente. 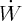 > 0 ; W
augmente aussi. V augmentera donc de plus en plus rapidement, jusqu’à V = 1 où
> 0 ; W
augmente aussi. V augmentera donc de plus en plus rapidement, jusqu’à V = 1 où
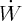 = 0 .
Ensuite, W diminue, et V augmente de moins en moins vite,
= 0 .
Ensuite, W diminue, et V augmente de moins en moins vite, 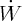 devenant de
plus en plus négatif. On arrive alors nécessairement en un point où W = 0,
donc où la tangente est verticale. Remarquons maintenant que le flot est
symétrique pour la transformation u
devenant de
plus en plus négatif. On arrive alors nécessairement en un point où W = 0,
donc où la tangente est verticale. Remarquons maintenant que le flot est
symétrique pour la transformation u  -u, W
-u, W  -W et V
-W et V  V . On dit que
le système est réversible. L’orbite retourne donc à l’origine par symétrie
par rapport à l’axe des V , en arrivant par la variété stable. D’où le dessin
ci-dessous.
V . On dit que
le système est réversible. L’orbite retourne donc à l’origine par symétrie
par rapport à l’axe des V , en arrivant par la variété stable. D’où le dessin
ci-dessous.
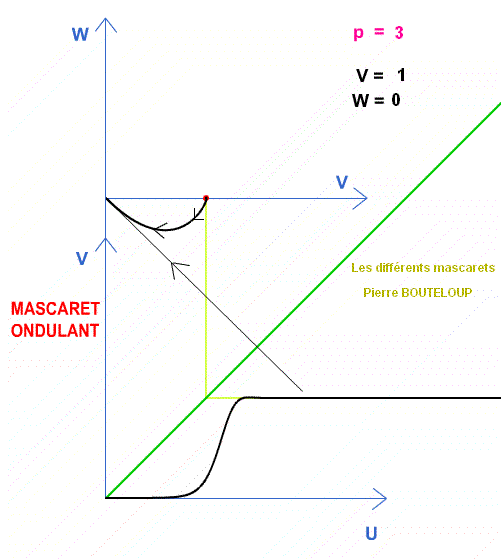
IV- Étude du cas p < 4 : mascaret ondulant
1- Maximum de E au point fixe (1,0)
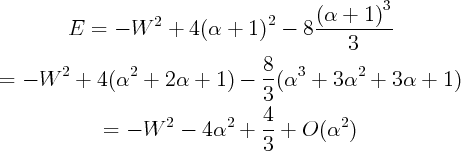
E est donc maximale au point fixe 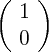 .
.
Pour W = 0 E = 4V 2 -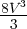 . Étudions la fonction y = 4x2 -
. Étudions la fonction y = 4x2 -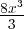 ;
y' = 8x(1 - x).
;
y' = 8x(1 - x).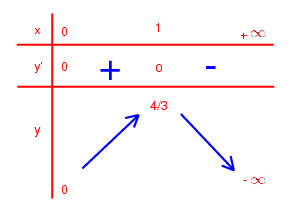
2- Décroissance de E au cours du mouvement sur la trajectoire
E = 4V 2 - 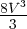 - W2. Rappelons que p > 0.
- W2. Rappelons que p > 0.
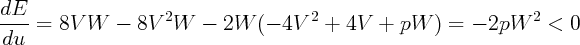
3- Lieu des points où 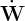 = 0
= 0
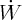 = 0
= 0
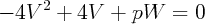
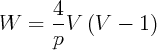
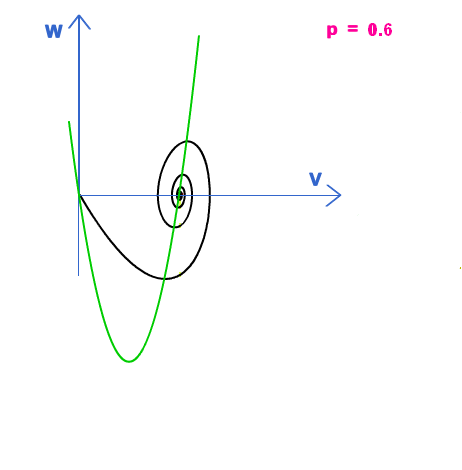
4- Trajectoire dans l’espace des phases, reliant les deux points fixes, pour 0 < p < 4
Remarquons tout d’abord, d’après le II, que la trajectoire, en remontant vers les u décroissants, se termine par une spirale. Il y a donc toujours oscillation pour V quand on tend vers le deuxième point fixe.
Remontons donc vers les u décroissants à partir de l’origine sur l’orbite
correspondant à la variété stable. V > 0 W < 0. 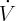 négatif, donc V augmente
lorsque u décroît. La pente à l’origine de la parabole vaut -
négatif, donc V augmente
lorsque u décroît. La pente à l’origine de la parabole vaut -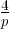 , tandis que pour la
trajectoire, on a :
, tandis que pour la
trajectoire, on a : 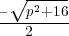 qui est plus grand que -
qui est plus grand que -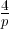 . La trajectoire est donc à
l’intérieur de la parabole.
. La trajectoire est donc à
l’intérieur de la parabole. 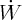 est positif. Donc la trajectoire descend et nécessairement
rencontre la parabole, et c’est là que la tangente est horizontale (
est positif. Donc la trajectoire descend et nécessairement
rencontre la parabole, et c’est là que la tangente est horizontale (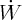 = 0). La
trajectoire ne peut recouper une deuxième fois la parabole en restant en dessous de
l’axe des V , car il y aurait un point à tangente verticale qui ne serait pas sur l’axe
des V , ce qui est impossible. La trajectoire ne peut pas non plus arriver
directement au deuxième point fixe, car au voisinage de ce dernier, la trajectoire est
en spirale (voir le II). Par conséquent, la trajectoire coupe l’axe des V à
l’extérieur de la parabole, puis remonte en partant à gauche (
= 0). La
trajectoire ne peut recouper une deuxième fois la parabole en restant en dessous de
l’axe des V , car il y aurait un point à tangente verticale qui ne serait pas sur l’axe
des V , ce qui est impossible. La trajectoire ne peut pas non plus arriver
directement au deuxième point fixe, car au voisinage de ce dernier, la trajectoire est
en spirale (voir le II). Par conséquent, la trajectoire coupe l’axe des V à
l’extérieur de la parabole, puis remonte en partant à gauche (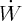 < 0 et
< 0 et 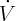 > 0).
La trajectoire recoupe donc la parabole, puis redescend en allant à gauche.
La tangente est verticale au point où l’axe des V est de nouveau coupé, et
on est ramené qualitativement à la même trajectoire que précédemment,
mais plus près du deuxième point fixe, puisque la fonction de Liapunov E
est constamment croissante quand on remonte les u. On voit donc que la
trajectoire est une spirale qui tend vers le deuxième point fixe, et que V
oscille.
> 0).
La trajectoire recoupe donc la parabole, puis redescend en allant à gauche.
La tangente est verticale au point où l’axe des V est de nouveau coupé, et
on est ramené qualitativement à la même trajectoire que précédemment,
mais plus près du deuxième point fixe, puisque la fonction de Liapunov E
est constamment croissante quand on remonte les u. On voit donc que la
trajectoire est une spirale qui tend vers le deuxième point fixe, et que V
oscille.