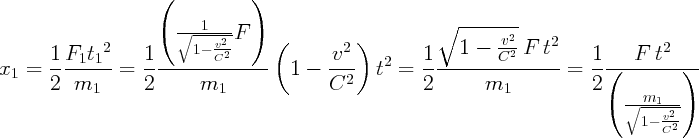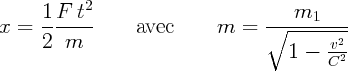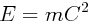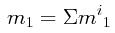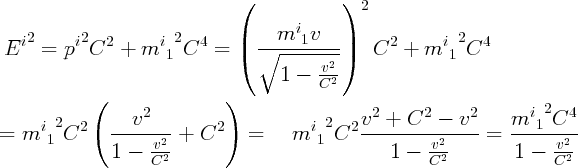LE PRINCIPE DE L’ACTION ET DE LA RÉACTION NE
S’APPLIQUE PAS, QUAND ON S’ENFONCE DANS UN CHAMP
GRAVITATIONNEL
Il y a une petite subtilité tout de même : le débit de photons virtuels vu par les
charges de la circonférence est plus grand d’un facteur 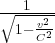 par rapport au débit de
photons virtuels vu par la charge q sur l’axe ; ceci du fait du ralentissement de
l’écoulement du temps sur la circonférence. v est la vitesse d’un point de la
circonférence.
par rapport au débit de
photons virtuels vu par la charge q sur l’axe ; ceci du fait du ralentissement de
l’écoulement du temps sur la circonférence. v est la vitesse d’un point de la
circonférence.
D’autre part, la composante de leur impulsion parallèlement à l’axe n’est pas
modifiée, car lorsqu’on se déplace parallèlement à l’axe, l’écoulement du temps ne
varie pas. Chaque photon délivre donc la même quantité de mouvement lorsqu’il est
absorbé.
La composante sur l’axe de la force subie par le cercle de charges est donc plus
grande d’un facteur 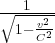 par rapport à la force subie par la charge q sur l’axe. Dans
le référentiel tournant, les forces subies par la charge q sur l’axe et par le cercle de
charges n’obéissent donc pas au principe de l’action et de la réaction.
par rapport à la force subie par la charge q sur l’axe. Dans
le référentiel tournant, les forces subies par la charge q sur l’axe et par le cercle de
charges n’obéissent donc pas au principe de l’action et de la réaction.
La
circonférence chargée est plus poussée vers la gauche que la charge q (à la droite de la
spire) est poussée vers la droite.
La mise en mouvement de la circonférence vers la gauche est donc vue plus forte,
mais dans un référentiel où le temps est ralenti ! Si la circonférence fait partie d’une
roue solide dont le pivot se trouve sur l’axe, au niveau du pivot, l’écoulement du
temps est le même qu’au niveau de la charge q. La force est donc bien exactement
opposée à la force subie par la charge q, mesurée par un observateur sur l’axe !
Il n’y a donc aucune ambiguïté pour évaluer la force électrostatique
subie par la charge q dans le référentiel tournant, puisque le principe de
l’action et de la réaction est alors vérifié et que les deux forces ressenties ont la
même intensité. Dans le référentiel tournant, la charge q est bien soumise
à la force donnée par la loi de Coulomb de l’électrostatique ; les distances,
rappelons le, n’étant pas modifiées par rapport à celles dans le référentiel fixe
(distances dans un plan méridien).
Comme il n’y a pas de changement de
l’écoulement du temps pour la charge q quand on passe d’un référentiel à l’autre,
l’accélération de q calculée dans les deux référentiels est la même. La force
électrostatique calculée dans les deux référentiels est la même d’après l’invariance
de la charge électrique et la non modification des distances dans un plan
méridien. La force magnétique est donc nulle pour la charge q dans le référentiel
fixe.

Examinons maintenant la loi de mouvement de la circonférence dans les deux
référentiels (R1 ) tournant et (R) fixe.
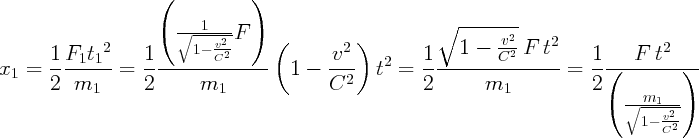 mais x = x1
mais x = x1
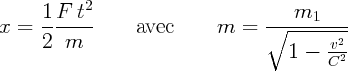
F est bien la même intensité de force que celle vue par la charge q et calculée en
pure théorie électrostatique ! On voit une augmentation de l’inertie de la circonférence
dans le référentiel fixe due à l’augmentation de son énergie. On retrouve bien la
fameuse formule d’Einstein 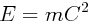 qui montre que la masse, donc l’inertie d’un objet
globalement immobile, c’est à dire de quantité de mouvement totale nulle, augmente
avec son énergie. Montrons que l’on retrouve sur ce cas particulier la relation
mathématique relativiste entre l’énergie, la quantité de mouvement p et la masse pour
un point matériel de la circonférence. Ici, mi1 est la masse d’un point matériel de la
circonférence ;
qui montre que la masse, donc l’inertie d’un objet
globalement immobile, c’est à dire de quantité de mouvement totale nulle, augmente
avec son énergie. Montrons que l’on retrouve sur ce cas particulier la relation
mathématique relativiste entre l’énergie, la quantité de mouvement p et la masse pour
un point matériel de la circonférence. Ici, mi1 est la masse d’un point matériel de la
circonférence ;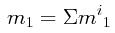
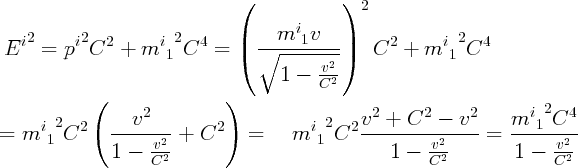
et en sommant :

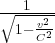 par rapport au débit de
photons virtuels vu par la charge q sur l’axe ; ceci du fait du ralentissement de
l’écoulement du temps sur la circonférence. v est la vitesse d’un point de la
circonférence.
par rapport au débit de
photons virtuels vu par la charge q sur l’axe ; ceci du fait du ralentissement de
l’écoulement du temps sur la circonférence. v est la vitesse d’un point de la
circonférence.