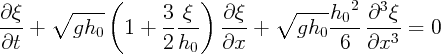
KORTEWEG-DE VRIES-BURGERS
K-dV :
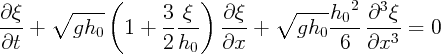
 ; devient, lorsqu’on ajoute un terme de dissipation, l’équation de
K-dV-Burgers :
; devient, lorsqu’on ajoute un terme de dissipation, l’équation de
K-dV-Burgers :
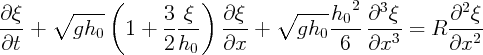
Posons : X = x - C0t (on avance avec la vitesse des ondes de faibles amplitudes) ;
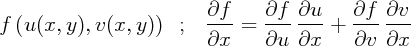
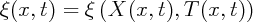
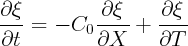
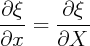
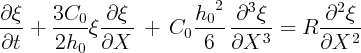
Posons : x1 = 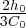 X ; il vient :
X ; il vient :
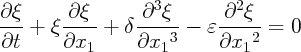
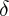 = 4/81
= 4/81 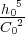 et
et 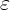 = R
= R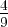
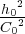 .
.
On cherche des solutions sous la forme d’ondes progressives avançant à la vitesse C :
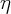 = x1 - Ct ;
= x1 - Ct ; 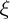 =
= 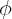 (
(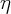 ).
).
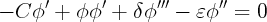
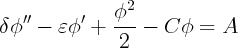
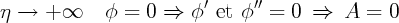
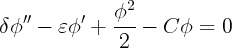
Une solution particulière est : 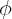 = 2C ; on pose
= 2C ; on pose 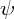 =
= 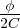 .
.
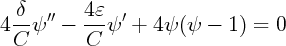
On pose : u = 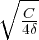
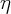 et p =
et p = 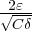 et on obtient l’équation :
et on obtient l’équation :
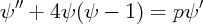
On résout ensuite dans le plan le système :
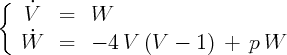
On peut théoriquement connaître la structure des solutions, mais une intégration numérique donne rapidement le résultat (animation précédente).