IV- Équilibre thermique

1) Deux molécules identiques

Deux molécules identiques enfermées dans une boîte et qui s’entrechoquent, voient, par raison de symétrie, statistiquement, leurs vitesses moyennes s’égaliser; également bien sûr, leurs énergies cinétiques. L’animation ci-contre (huitième animation) le montre, et permet d’évaluer le temps qu’il faut pour que cet équilibre se réalise, ainsi que les fluctuations, c’est à dire les écarts à l’équilibre que le système subit.
        On voit que les fluctuations relatives, sont de l’ordre de grandeur de ; N étant le nombre de chocs subi.

2) Deux particules de masses différentes (m_rouge = 4m_verte)

Dans ce cas, la particule la plus lourde va systématiquement moins vite. Mais on peut démontrer, et on constate sur l’animation ci-contre (neuvième animation) que l’énergie moyenne des deux boules tend à être égale, la diminution de la vitesse au carré étant compensée multiplicativement par l’augmentation de la masse. Il s’agit de l’établissement de l’équilibre thermique. La température est en effet proportionnelle à l’énergie cinétique (liée au mouvement) moyenne d’une molécule quelconque. Pour un gaz parfait monoatomique (les molécules sont des atomes seuls) :

T est la température absolue mesurée en Kelvin et k_B = 1.38 10^-23 est la constante de Boltzmann. La masse m est mesurée en kg et la vitesse en m/s.

3) Intervention de la gravité

Si les boules sont attirées par la Terre, la plus lourde allant moins vite, est en moyenne à une altitude plus faible (dixième animation ci-contre). On verra ci-dessous (loi d’Avogadro) que dans un volume donné, il y a toujours le même nombre de molécules, quelle que soit la nature du gaz. La densité d’un gaz est donc proportionnelle à la masse de ses molécules. On voit ainsi qu’un gaz léger (peu dense) à tendance à se placer au dessus d’un gaz lourd.

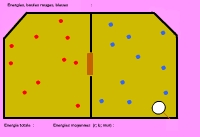
4) Établissement de l’équilibre thermique

Dans l’animation ci-contre (onzième animation), deux compartiments égaux en volume et nombre de molécules échangent de la chaleur par des chocs avec un piston mobile. On voit peu à peu s’établir l’équilibre thermique qui a lieu quand les deux compartiments ont la même énergie. En fait, c’est les températures qui s’égalisent, de telle sorte que si un des deux compartiments avait deux fois plus de molécules, il aurait à l’équilibre une énergie double.

D’une manière générale, si on met en équilibre thermique un gaz contenant N₁ molécules à la température T₁ avec un autre gaz contenant N₂ molécules à la température T₂ > T₁, la température finale T_f est telle que : N₁ (T₁ - T_f ) = N₂ (T_f -T₂) puisque l’énergie donnée par l’un (chaleur) est égale à celle reçue par l’autre. On obtient :

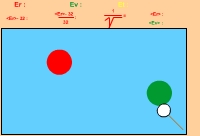
5) Cas de trois boules, une chaude et deux froides

Le calcul ci-dessus est mis en application dans l’animation ci-contre (douzième animation) où N₁ = 1;
T₁ = 80; N₂ = 2; T₂ = 20. Les deux boules vertes ont la même masse et la même température. La boule rouge a une masse quatre fois plus grande que celle d’une boule verte.

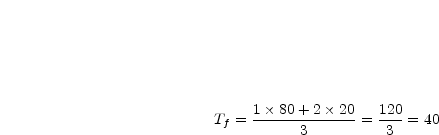
L’animation affiche l’énergie moyenne calculée au cours du temps pour chaque molécule. Pour la boule rouge par exemple :

avec : t = t₁ + t₂ + ...t_n.
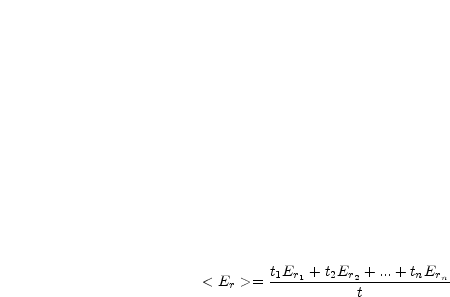
        t₁ est le temps qui s’écoule entre le choc i - 1 et le choc i pour la boule considérée.

Il faut cliquer sur départ pour commencer les chocs, et la remise à 0 signifie qu’on recalcule les valeurs moyennes à partir de l’instant où l'on a cliqué.

Suite : loi d’Avogadro