IX- Déduction de la loi de force de la relativité
1) Construction des théories scientifiques
Dans le paragraphe
1 du
chapitre VI,
nous avons présenté expérimentalement la loi de force. Il est satisfaisant de voir
que cette loi de force découle bien de l'alliance de la relativité d'Einstein avec l'électrostatique,
dans la logique de la démarche du
chapitre V; c'est ce que nous faisons dans ce chapitre.
On peut en effet montrer rigoureusement que les lois de l'électrostatique, alliées à la relativité, donnent les lois de l'électromagnétisme,
donc la magnétostatique également. Sans les mathématiques, on ne peut pas le montrer rigoureusement; quelques arguments permettent toutefois d'arriver à
la loi
de force de la magnétostatique :
Les théories scientifiques ne se construisent pas par induction à partir des faits expérimentaux comme l'ont montré le philosophe Hume puis,
plus récemment, le philosophe Karl Popper. Elles sont une création de l'esprit humain, mais peuvent être falsifiées, c'est à dire réfutées par
l'expérience.
Cependant, les scientifiques ne partent pas de rien pour imaginer une théorie. Ils procèdent par analogie, ou par généralisation d'une idée qui est
manifeste dans un cas particulier, ou une expérience simple. Dans cette démarche, la méthode dite du "rasoir d'Occam" est utilisée. Il s'agit de
construire la théorie la plus simple possible qui puisse rendre compte de tous les faits expérimentaux.
2) Le champ magnétique
Dans cette attitude, on peut postuler que tous les effets magnétiques peuvent être obtenus
avec une simple spire en rotation chargée
uniformément avec un seul type de charges; c'est à dire que l'état magnétique le plus général en un point, peut être obtenu avec une spire parcourue par
un courant, dont le point considéré est le centre.
Revenons à la spire chargée, c'est à dire en fait un cercle constitué d'une matière isolante, sur lequel on a placé uniformément des charges
négatives (des électrons). On choisit alors toujours la même spire, c'est à dire que le rayon est toujours le même, et que la charge totale est toujours
la même. Tout état magnétique en un point peut alors être obtenu en plaçant le centre de cette spire au point considéré, et en la faisant tourner à la vitesse
adéquat autour d'un axe adéquat. On voit que l'état magnétique est alors caractérisé par le vecteur rotation de cette spire, qui est porté par l'axe,
en étant plus ou moins intense, dans un sens ou dans l'autre (deux sens de rotations possibles).
On a ainsi défini le vecteur champ magnétique.
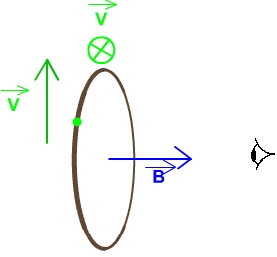
Si on fait une bousssole avec une spire, on se rend compte que, vu du pôle nord de cette spire, on voit les électrons tourner dans le
sens des aiguilles d'une montre. Par convention, le champ magnétique pointe du pôle sud vers le pôle nord. Tout cela est résumé sur la figure à droite.
Par raison de symétrie, en tout point de l'axe, le champ magnétique sera encore porté par l'axe.
3) Action d'un champ magnétique sur une charge de vitesse nulle ou parallèle au champ magnétique
La charge
q peut être choisie sur l'axe de la spire chargée précédente, et
si elle bouge, sa vitesse est alors portée par l'axe de la spire. La charge
parcourt donc l'axe de la spire. Plaçons nous alors dans le référentiel tournant où les charges électrostatiques de la spire sont immobiles.
On est alors en face d'un pur problème d'électrostatique. La distance commune
d des électrons à la charge
q est la même que dans
le référentiel fixe, car il n'y a pas de contraction des longueur perpendiculairement au mouvement. La force électrostatique subie
par la charge
q dans le référentiel
tournant est donc, compte tenu de l'invariance de la charge électrique, la même que dans le référentiel fixe. De là, on calcule l'accélération
de la charge qui est bien portée, par symétrie, par l'axe. Or, dans le référentiel fixe, sur l'axe, le temps s'écoule à la même vitesse que dans
le référentiel mobile (ce n'est pas le cas en dehors de l'axe). L'accélération, donc la force, vues dans le référentiel fixe, sont donc les même que
dans le référentiel mobile,
donc les mêmes qu'en électrostatique pur.
La force magnétique à laquelle est soumise une charge dont la vitesse est parallèle au champ magnétique est donc nulle.
Autrement dit : la force subie par la charge
q dans le référentiel fixe est-elle modifiée par la mise en rotation de la spire
chargée, ce qui correspondrait à l'apparition d'une force magnétique? Non, en effet, dans le référentiel tournant, on a toujours affaire à un problème
d'électrostatique et la force n'est pas modifiée lors de la mise en rotation, du fait du non changement des distances qui interviennent, et de l'invariance de la charge électrique,
donc du non changement de cette dernière. L'accélération dans le référentiel tournant n'est donc pas modifiée; mais elle
est identique à l'accélération dans le référentiel fixe, puisque sur l'axe
le temps s'écoule à la même vitesse dans les deux référentiels. Cette dernière accélération n'est donc pas modifiée, par conséquent, la force subie
n'est pas modifiée.
Il y a tout
de même une petite subtilité due au fait que le temps ne s'écoule pas à la même vitesse pour les points de l'axe et pour les points de la spire.
Nous renvoyons à ce
lien pour voir que cette subtilité ne modifie pas la validité du raisonnement précédent.
4) Force magnétique subie par une charge dont la vitesse est perpendiculaire au champ magnétique
Intéressons nous en préalable au champ magnétique en dehors de l'axe de la spire.
Les spectres d'aimants donnant bien un champ porté par l'axe sur l'axe, on peut leur
faire confiance dans cette démarche heuristique pour connaître le champ en dehors de l'axe et ainsi la composante non portée
par l'axe du champ magnétique.
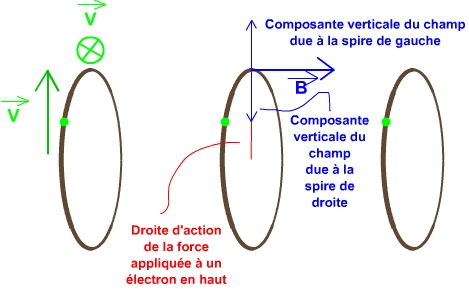
Considérons, sur la figure à droite, trois spires neutres identiques,parcourues par des courants identiques. La spire du milieu est
attirée magnétiquement vers la gauche par la spire de gauche, et avec la même intensité, vers la droite par la spire de droite
(voir le chapitre V sur l'unification de l'électricité et du magnétisme). Au niveau des électrons de la spire du milieu, le champ
magnétique créé par les deux autres spires
est porté par l'axe commun des trois spires. En effet, les composantes horizontales des deux spires à droite et à gauche s'ajoutent,
et les composantes verticales se retranchent, comme on le voit sur la figure. Il n'y a pas augmentation ou diminution du courant dans la spire du milieu,
car ce serait contraire à la conservation de l'énergie. Donc, les électrons ne sont pas soumis à une force tangentielle. La seule force
possible à laquelle ils puissent être soumis est une force radiale, donc perpendiculaire à la vitesse des charges et au champ magnétique.
Il nous reste à déterminer le sens de cette force en fonction du sens de la vitesse et du sens du champ magnétique.
5) Loi de force en magnétostatique
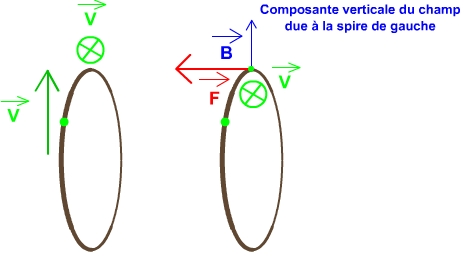
Pour avoir complètement accès à la loi de force, revenons à deux spires neutres parcourues par des courants identiques. On sait
d'après le chapitre V qu'elles s'attirent magnétiquement. La force est donc horizontale. C'est donc forcément la composante verticale du champ
magnétique créé par la spire de gauche qui agit en haut par exemple, sur la spire de droite.
Sur la figure ci-contre, on connait donc la force, la vitesse et le champ magnétique, donc la loi de force.
Pour une vitesse quelconque, on la décompose en une composante sur le champ magnétique et une composante perpendiculairement, et seule
la composante perpendiculaire donne une force, dont on suppose qu'elle est la même que si la vitesse était réduite à cette seule composante
perpendiculaire au champ magnétique.